C 언어 코딩 도장

지금까지 정수를 변수에 저장했습니다.이번에는 소수점을 표현할 수 있는 실수를 변수에 저장해보겠습니다.

다음은 실수 자료형의 크기와 저장할 수 있는 값의 범위입니다(여기 나오는 모든 내용을 외울 필요는 없습니다. 실수 자료형의 크기 정도만 기억하면 되고, 나머지는 나중에 필요할 때 찾아보세요).

자료형	크기	범위	유효자릿수	비고
float	4바이트, 32비트	1.175494e-38~3.402823e+38	7	IEEE 754 단정밀도 부동소수점
double	8바이트, 64비트	2.225074e-308~1.797693e+308	16	IEEE 754 배정밀도 부동소수점
long double	8바이트, 64비트	2.225074e-308~1.797693e+308	16	IEEE 754 배정밀도 부동소수점

참고 | 지수 표기법

아주 큰 숫자나 아주 작은 숫자를 표기할 때는 지수 표기법(exponential notation)을 사용합니다. 지수 표기법은 과학적 표기법(scientific notation)이라고도 부릅니다.

• 실수e+지수: 실수 * 10의 거듭제곱입니다. 2.1e+3이라면 2.1 * 1000 = 2100이 됩니다.
• 실수e-지수: 실수 * (1 / 10의 거듭제곱)입니다. 2.1e-2라면 2.1 * (1/100) = 0.021이 됩니다.

참고 | long double

long double은 운영체제와 플랫폼마다 크기가 다릅니다.

운영체제	CPU(플랫폼)	바이트 크기	비트 크기
Windows	x86(32비트)	8	64
	x86-64(64비트)	8	64
리눅스	x86(32비트)	12	96
	x86-64(64비트)	16	128
OS X	x86(32비트)	16	128
	x86-64(64비트)	16	128

64비트 리눅스, OS X에서는 IEEE 754 4배정도 부동소수점을 저장할 수 있습니다(3.362103e-4932~1.189731e+4932).

지금부터 설명할 부동소수점 규약은 참고삼아 읽어보면 됩니다. 실제로 부동소수점 규약을 완벽하게 외우는 프로그래머는 많지 않으며 수치에 민감한 과학, 공학 분야가 아니면 보통 잘 모릅니다. 특히 부동소수점 규약을 몰라도 C 언어로 프로그램을 만드는 데는 문제가 없습니다. 우선은 프로그래밍을 쉽고 즐겁게 배우는 것이 중요합니다.

컴퓨터에서는 값을 0과 1로 저장합니다. 그래서 실수도 0과 1로 저장해야 하는데 이렇게 실수와 소수점을 2진수로 표현하는 방식을 부동소수점 표현 방식이라고 합니다. 부동소수점 방식은 자료형의 일정 부분을 비트 단위로 나누어 부호, 가수(significand), 기수(base), 지수(exponent)를 저장하여 실수를 표현합니다.

부동소수점은 다음과 같이 기수(n)를 지수(p)만큼 거듭제곱한 값을 가수(m)와 곱하는 방식을 사용합니다. 단, 컴퓨터는 값을 저장할 때 2진수로 저장하므로 기수(밑수)는 2로 고정되어 있으며 2 자체는 따로 저장하지 않습니다.

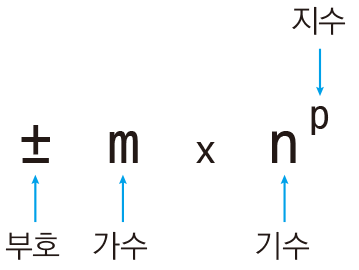
부동소수점 저장에 관한 규약은 IEEE 754라는 표준으로 정해져 있습니다. 다음은 IEEE 754에서 단정밀도 부동소수점인 float와 배정밀도 부동소수점인 double의 저장 방식입니다.

자료형	크기	부호	지수	가수
float	32비트	1비트	8비트	23비트
double	64비트	1비트	11비트	52비트

유효자릿수는 실수를 일정 자릿수만큼만 표현할 수 있다는 뜻입니다. 만약 유효자릿수가 7이라면 0.123456789는 반올림하여 0.123457로 표시됩니다. 즉, 정수 부분 1자리와 소수 부분 6자리로 7자리가 표시됩니다.

단정밀도와 배정밀도 부동소수점은 저장할 수 있는 크기가 다르므로 유효자릿수의 차이가 있습니다. 따라서 배정밀도 부동소수점이 좀 더 긴 자릿수의 소수점을 정밀하게 표현할 수 있습니다.

읽을거리

실수 자료형은 3D 게임을 만들 때 많이 사용합니다. 특히 3차원 좌표에는 float를 주로 사용하며 여기에 행렬을 곱하여 이동, 회전, 확대 축소 등을 하게 됩니다. 만약 3D 게임 엔진을 공부하고 싶다면 실수 자료형을 눈에 익혀두는것이 좋습니다.

특히 3D 게임 엔진은 많은 부분이 수학으로 이루어져 있습니다. 행렬 곱셈 한 번만으로 이동, 회전, 확대 축소(scale)를 할 수 있는 연산을 아핀 변환(affine transformation)이라고 하는데 아핀 변환은 선형대수학 과목에서 배울 수 있습니다.