C 언어 코딩 도장: 50.1 두 점 사이의 거리 구하기

50 두 점 사이의 거리 구하기

구조체의 기본 문법을 알아보았으니 이번에는 구조체를 활용하여 2차원 평면에서 위치를 표현한 뒤 두 점 사이의 거리를 구해보겠습니다.

50.1 두 점 사이의 거리 구하기

2차원 평면에서 위치를 표현하려면 x와 y값이 필요하겠죠? 지금까지 봐온 Point2D 구조체를 활용해보겠습니다.

struct Point2D {
    int x;
    int y;
};

이제 구조체로 변수 두 개를 선언하여 점 두 개를 표현합니다.

two_point.c

#include <stdio.h>

struct Point2D {
    int x;
    int y;
};

int main()
{
    struct Point2D p1;    // 점1
    struct Point2D p2;    // 점2

    // 점1 위치
    p1.x = 30;
    p1.y = 20;

    // 점2 위치
    p2.x = 60;
    p2.y = 50;

    printf("p1: %d %d\n", p1.x, p1.y);    // 30 20
    printf("p2: %d %d\n", p2.x, p2.y);    // 60 50

    return 0;
}

실행 결과

p1: 30 20
p2: 60 50

2차원 평면에서 점을 표시해보면 다음처럼 됩니다.

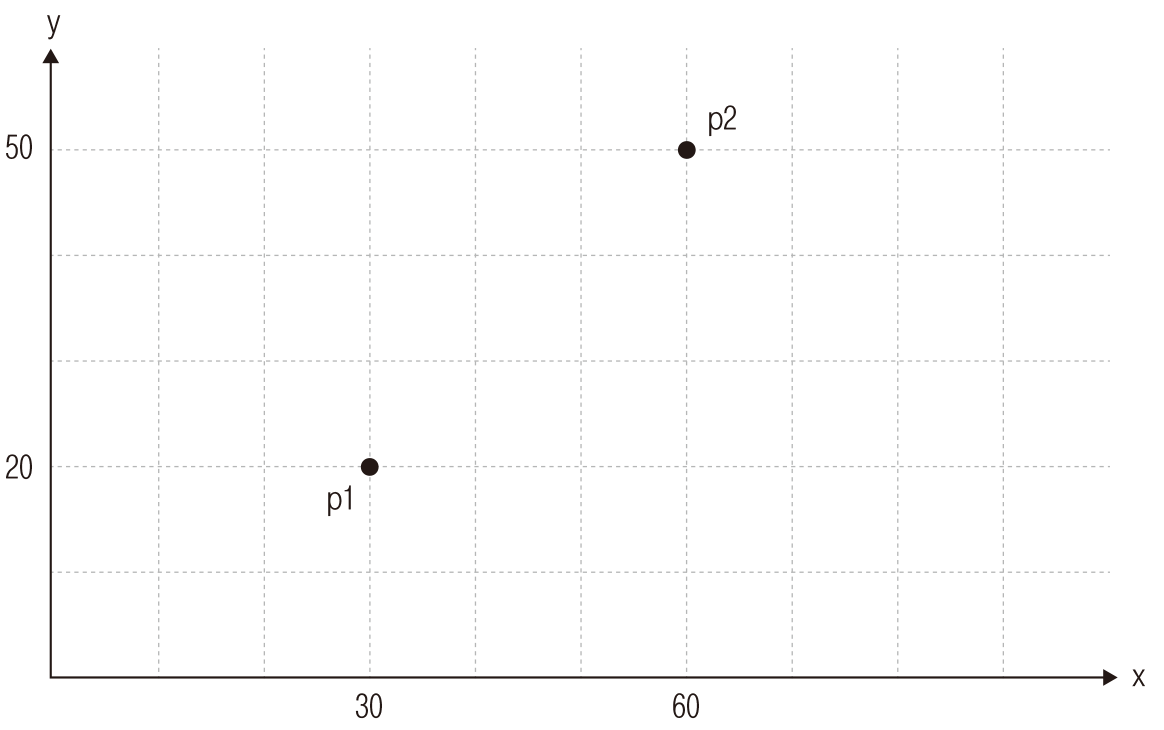
두 점의 거리를 구하려면 어떻게 해야 할까요? 학교에서 배운 피타고라스의 정리를 이용하면 됩니다.

임의의 직각삼각형에서 빗변을 한 변으로 하는 정사각형의 넓이는 다른 두 변을 각각 한 변으로 하는 정사각형의 넓이의 합과 같다.
a² + b² = c²

그럼 점 p1과 p2로 직각삼각형을 그려봅니다.

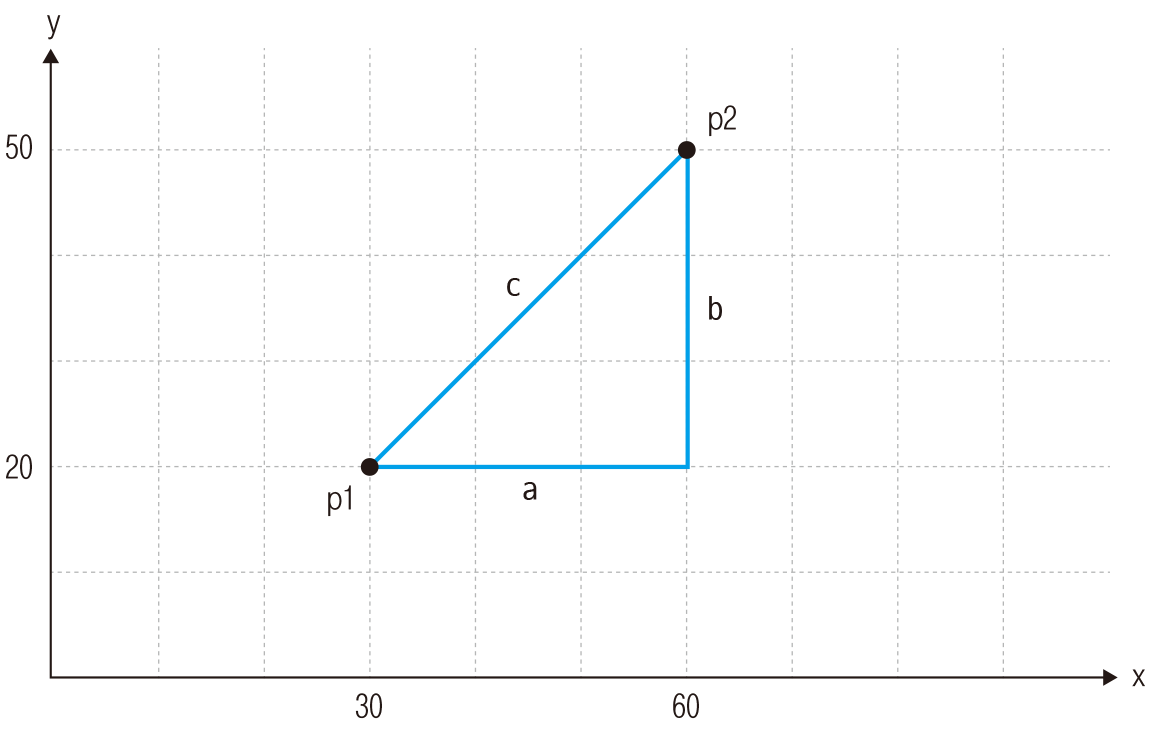
피타고라스의 정리에 대입하려면 먼저 선 a와 b의 길이를 구해야 합니다. 우리는 구조체 변수에 두 점의 좌표 정보가 들어있으므로 구조체 변수를 활용하면 됩니다.

int a = p2.x - p1.x;    // 선 a의 길이
int b = p2.y - p1.y;    // 선 b의 길이

a는 p2의 x에서 p1의 x를 빼면 되고, b는 p2의 y에서 p1의 y를 빼면 됩니다.

그다음에 피타고라스의 정리에서 c의 길이를 계산하려면 제곱근을 구해야 합니다.

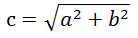
그럼 √(루트)는 어떻게 구현해야 할까요? 이때는 C 언어에서 제공하는 sqrt 함수를 사용하면 편리합니다. sqrt는 제곱근을 뜻하는 square root에서 따왔으며 math.h 헤더 파일에 선언되어 있습니다.

sqrt(값)

double sqrt(double _X);
제곱근을 반환, _X가 음수이면 NaN을 반환

참고 | GCC에서 sqrt 함수 사용하기

GCC에서 sqrt 함수를 사용하려면 컴파일 옵션에 -lm을 지정해야 합니다(-lm은 수학 라이브러리를 링크한다는 뜻).

$ gcc two_point_distance.c -o two_point_distance -lm

이제 sqrt 함수까지 사용해서 p1과 p2의 거리를 구해보겠습니다.

two_point_distance.c

#include <stdio.h>
#include <math.h>    // sqrt 함수가 선언된 헤더 파일

struct Point2D {
    int x;
    int y;
};

int main()
{
    struct Point2D p1;    // 점1
    struct Point2D p2;    // 점2

    // 점1 위치
    p1.x = 30;
    p1.y = 20;

    // 점2 위치
    p2.x = 60;
    p2.y = 50;

    int a = p2.x - p1.x;    // 선 a의 길이
    int b = p2.y - p1.y;    // 선 b의 길이

    double c = sqrt((a * a) + (b * b));    // (a * a) + (b * b)의 제곱근을 구함

    printf("%f\n", c);       // 42.426407

    return 0;
}

실행 결과

42.426407

sqrt 함수에 값을 넣으면 해당 값의 제곱근을 구해줍니다. 이때 제곱근은 소수로 나오므로 double형 변수에 저장해줍니다.

여기서는 a의 제곱과 b의 제곱의 합을 (a * a) + (b * b)처럼 표현했는데 거듭제곱(power)을 구하는 pow 함수를 사용해도 됩니다(math.h).

pow(값, 지수)

double pow(double _X, double _Y);
_X의 _Y 거듭제곱을 반환

즉, a²를 구하고 싶다면 pow(a, 2)처럼 사용합니다. 앞에서 작성한 코드를 pow 함수로 다시 작성하면 다음과 같은 모양이 되겠죠?

double c = sqrt(pow(a, 2) + pow(b, 2));

만약 선의 위치를 구할 때 p2에서 p1을 빼는 것이 아닌 p1에서 p2를 빼면 어떻게 될까요?

int a = p1.x - p2.x;    // 선 a의 길이
int b = p1.y - p2.y;    // 선 b의 길이

30 - 60은 -30이고 20 - 50도 -30입니다. 하지만 걱정하지 않아도 됩니다. a² + b² = c² 식에서 a와 b는 같은 값을 두 번 곱하는데 음수(-)끼리 곱하면 항상 양수(+)가 되므로 부호는 상관하지 않아도 됩니다. 즉, 양수(+) * 양수(+) 또는 음수(-) * 음수(-) 상황밖에 없기 때문이죠.

참고 | 절댓값 함수

abs, fabs, fabsf 함수를 사용하면 양수 또는 음수를 절댓값(absolute value)으로 만들 수 있습니다. 이 함수도 math.h 헤더 파일에 선언되어 있습니다.

abs(정수);

int abs(int _X);
정수 절댓값을 반환

fabs(double형 실수);

double fabs(double _X);
double형 실수 절댓값을 반환

fabsf(float형 실수);

float fabsf(float _X);
float형 실수 절댓값을 반환

지금까지 구조체를 사용하여 점을 표현하고 두 점 사이의 거리를 구하는 방법을 배웠는데 피타고라스의 정리를 수학 함수로 푸는 부분이 약간 어려웠습니다. 당장 이해가 되지 않는다면 일단 넘어가도 상관없습니다. 나중에 두 점 사이의 거리를 구해야 할 때 다시 돌아와서 찾아보세요.

C 언어 코딩 도장 생략내비게이션 생략