파이썬 코딩 도장: 26.2 집합 연산 사용하기

26.2 집합 연산 사용하기

이제 세트에서 집합 연산과 이에 대응하는 메서드를 사용해보겠습니다. 집합 연산은 파이썬의 산술 연산자와 논리 연산자를 활용합니다.

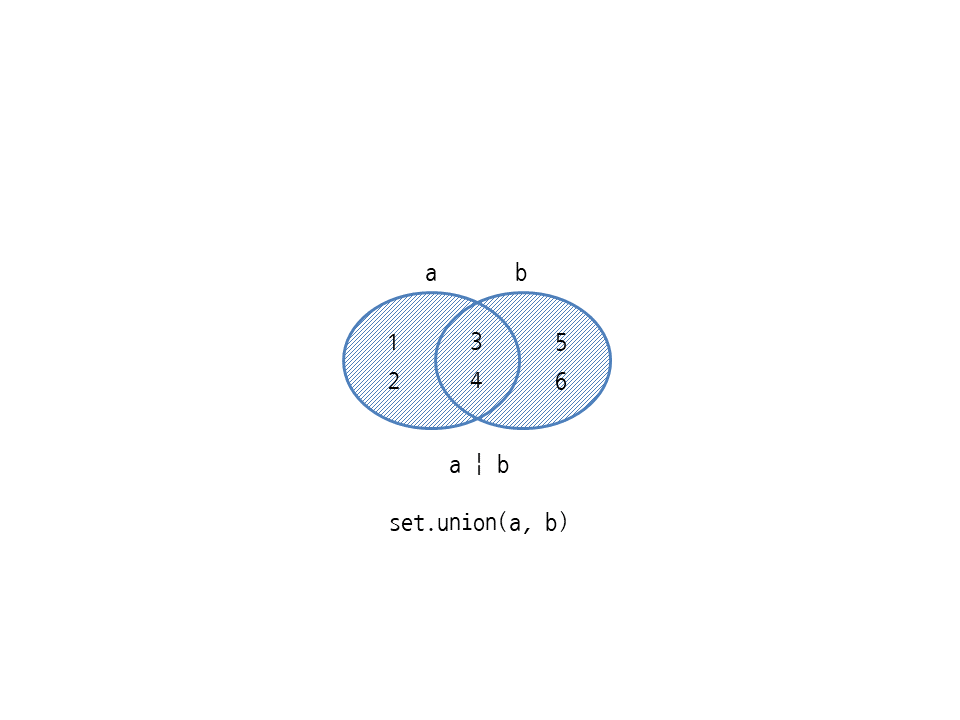
| 연산자는 합집합(union)을 구하며 OR 연산자 |를 사용합니다. set.union 메서드와 동작이 같습니다. 다음은 세트 {1, 2, 3, 4}와 {3, 4, 5, 6}을 모두 포함하므로 {1, 2, 3, 4, 5, 6}이 나옵니다.

세트1 | 세트2
set.union(세트1, 세트2)

>>> a = {1, 2, 3, 4}
>>> b = {3, 4, 5, 6}
>>> a | b
{1, 2, 3, 4, 5, 6}
>>> set.union(a, b)
{1, 2, 3, 4, 5, 6}

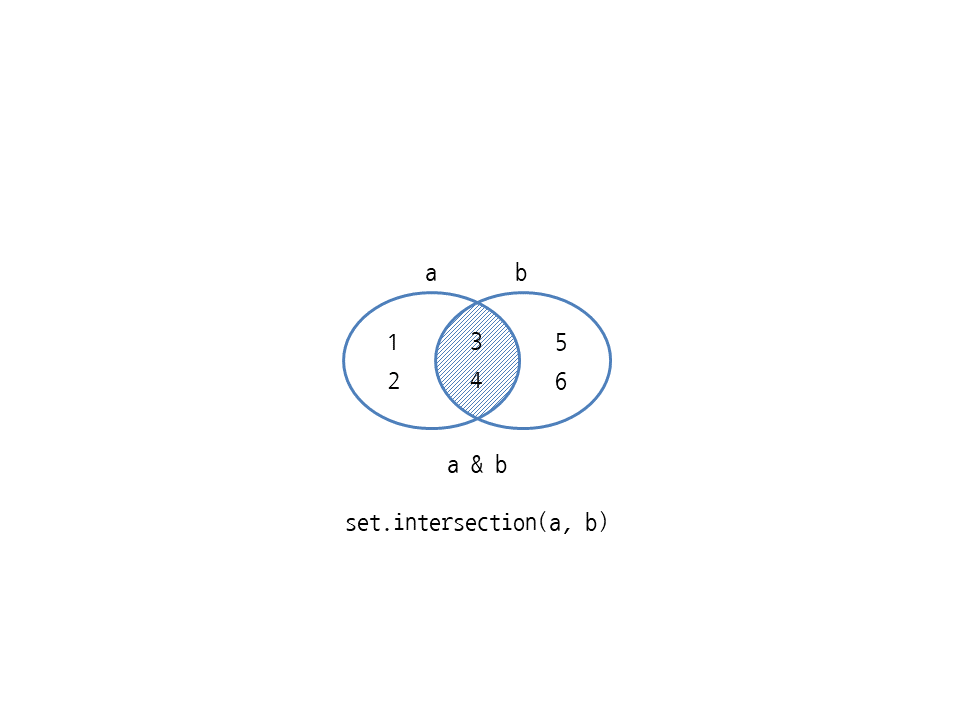
& 연산자는 교집합(intersection)을 구하며 AND 연산자 &를 사용합니다. set.intersection 메서드와 동작이 같습니다. 다음은 세트 {1, 2, 3, 4}와 {3, 4, 5, 6} 중에서 겹치는 부분을 구하므로 {3, 4}가 나옵니다.

세트1 & 세트2
set.intersection(세트1, 세트2)

>>> a & b
{3, 4}
>>> set.intersection(a, b)
{3, 4}

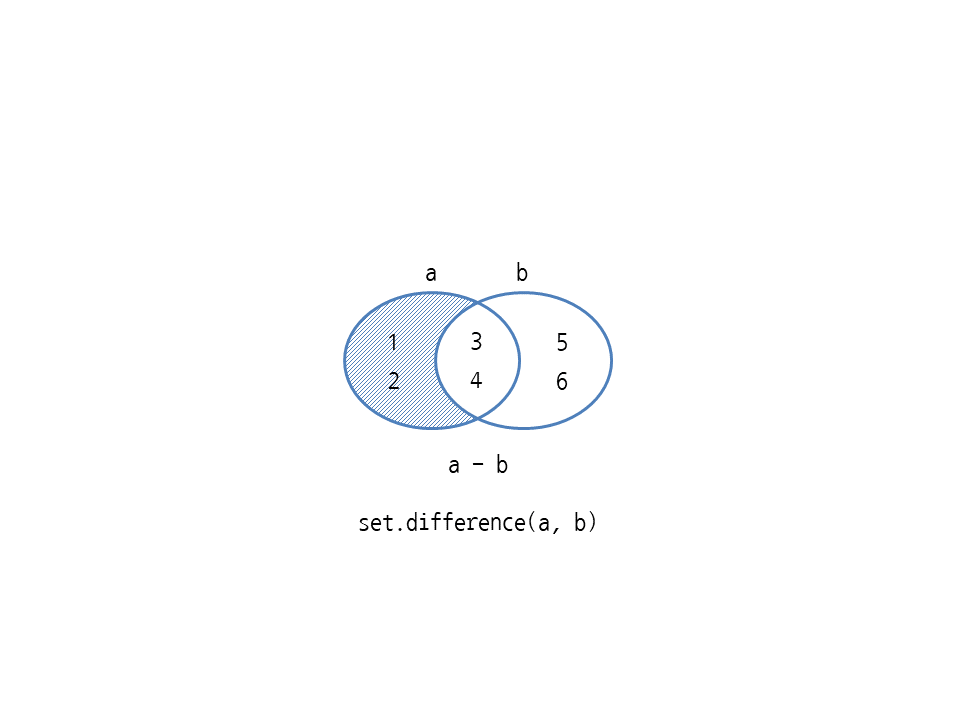
- 연산자는 차집합(difference)을 구하며 뺄셈 연산자 -를 사용합니다. set.difference 메서드와 동작이 같습니다. 다음은 {1, 2, 3, 4}에서 {3, 4, 5, 6}과 겹치는 3과 4를 뺐으므로 {1, 2}가 나옵니다.

세트1 - 세트2
set.difference(세트1, 세트2)

>>> a - b
{1, 2}
>>> set.difference(a, b)
{1, 2}

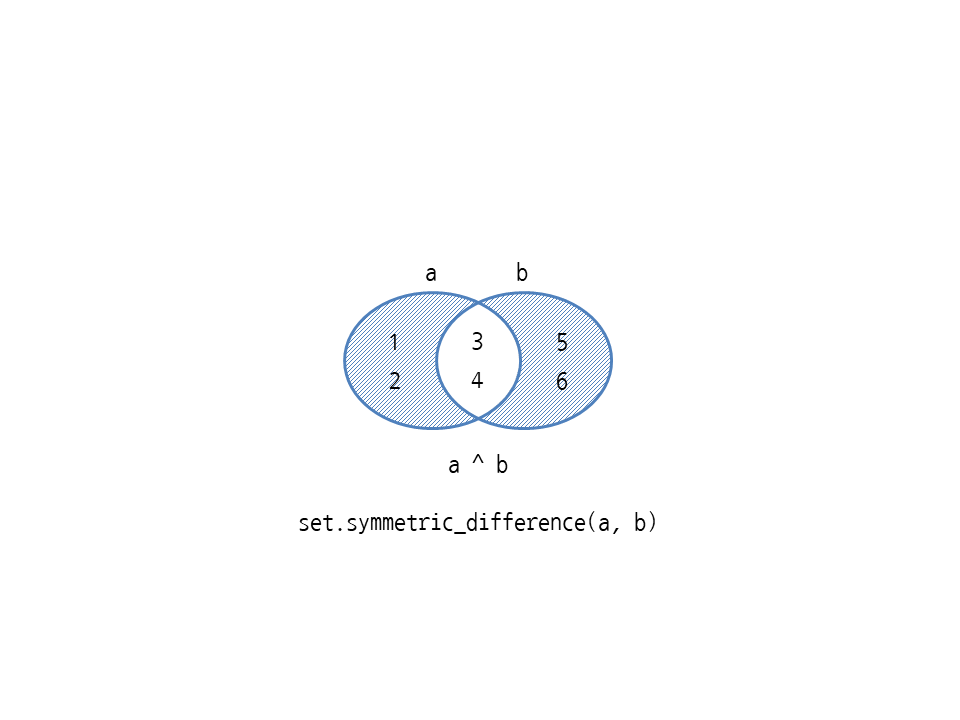
^ 연산자는 대칭차집합(symmetric difference)을 구하며 XOR 연산자 ^를 사용합니다. set.symmetric_difference 메서드와 동작이 같습니다.

대칭차집합은 XOR 연산자의 특성을 그대로 따르는데 XOR은 서로 다르면 참입니다. 따라서 집합에서는 두 집합 중 겹치지 않는 요소만 포함합니다. 다음은 세트 {1, 2, 3, 4}와 {3, 4, 5, 6} 중에서 같은 값 3과 4를 제외한 다른 모든 요소를 구하므로 {1, 2, 5, 6}이 나옵니다.

세트1 ^ 세트2
set.symmetric_difference(세트1, 세트2)

>>> a ^ b
{1, 2, 5, 6}
>>> set.symmetric_difference(a, b)
{1, 2, 5, 6}

26.2.1 집합 연산 후 할당 연산자 사용하기

이번에는 세트 자료형에 집합 연산 후 할당 연산자와 이에 대응하는 메서드를 사용해보겠습니다. 세트 자료형에 |, &, -, ^ 연산자와 할당 연산자 =을 함께 사용하면 집합 연산의 결과를 변수에 다시 저장(할당)합니다.

|=은 현재 세트에 다른 세트를 더하며 update 메서드와 같습니다. 다음은 세트 {1, 2, 3, 4}에 {5}를 더하므로 {1, 2, 3, 4, 5}가 나옵니다.

세트1 |= 세트2
세트1.update(세트2)

>>> a = {1, 2, 3, 4}
>>> a |= {5}
>>> a
{1, 2, 3, 4, 5}
>>> a = {1, 2, 3, 4}
>>> a.update({5})
>>> a
{1, 2, 3, 4, 5}

&=은 현재 세트와 다른 세트 중에서 겹치는 요소만 현재 세트에 저장하며 intersection_update 메서드와 같습니다. 다음은 세트 {1, 2, 3, 4}와 {0, 1, 2, 3, 4} 중에서 겹치는 요소만 a에 저장하므로 {1, 2, 3, 4}가 나옵니다.

세트1 &= 세트2
세트1.intersection_update(세트2)

>>> a = {1, 2, 3, 4}
>>> a &= {0, 1, 2, 3, 4}
>>> a
{1, 2, 3, 4}
>>> a = {1, 2, 3, 4}
>>> a.intersection_update({0, 1, 2, 3, 4})
>>> a
{1, 2, 3, 4}

-=은 현재 세트에서 다른 세트를 빼며 difference_update 메서드와 같습니다. 다음은 세트 {1, 2, 3, 4}에서 {3}을 빼므로 {1, 2, 4}가 나옵니다.

세트1 -= 세트2
세트1.difference_update(세트2)

>>> a = {1, 2, 3, 4}
>>> a -= {3}
>>> a
{1, 2, 4}
>>> a = {1, 2, 3, 4}
>>> a.difference_update({3})
>>> a
{1, 2, 4}

^=은 현재 세트와 다른 세트 중에서 겹치지 않는 요소만 현재 세트에 저장하며 symmetric_difference_update 메서드와 같습니다. 다음은 세트 {1, 2, 3, 4}와 {3, 4, 5, 6} 중에서 겹치지 않는 요소만 a에 저장하므로 {1, 3}이 나옵니다.

세트1 ^= 세트2
세트1.symmetric_difference_update(세트2)

>>> a = {1, 2, 3, 4}
>>> a ^= {3, 4, 5, 6}
>>> a
{1, 2, 5, 6}
>>> a = {1, 2, 3, 4}
>>> a.symmetric_difference_update({3, 4, 5, 6})
>>> a
{1, 2, 5, 6}

26.2.2 부분 집합과 상위집합 확인하기

세트는 부분집합, 진부분집합, 상위집합, 진상위집합과 같이 속하는 관계를 표현할 수도 있습니다. 현재 세트가 다른 세트의 (진)부분집합 또는 (진)상위집합인지 확인할 때는 세트 자료형에 부등호와 등호 사용합니다.

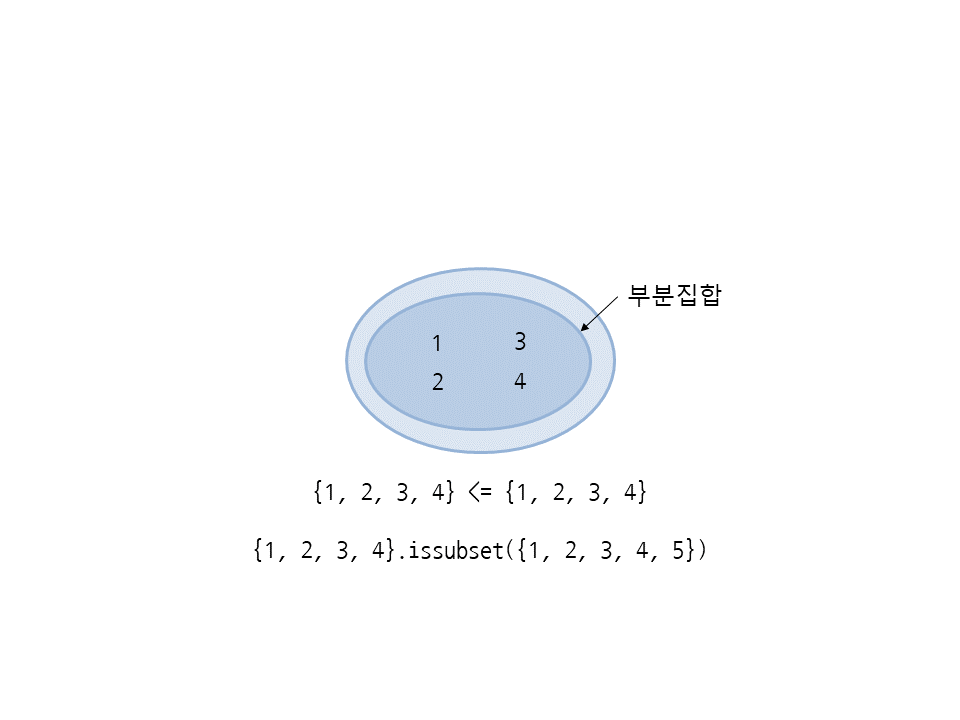
<=은 현재 세트가 다른 세트의 부분집합(subset)인지 확인하며 issubset 메서드와 같습니다. 다음은 세트 {1, 2, 3, 4}가 {1, 2, 3, 4}의 부분집합이므로 참입니다(등호가 있으므로 두 세트가 같을 때도 참입니다).

현재세트 <= 다른세트
현재세트.issubset(다른세트)

>>> a = {1, 2, 3, 4}
>>> a <= {1, 2, 3, 4}
True
>>> a.issubset({1, 2, 3, 4, 5})
True

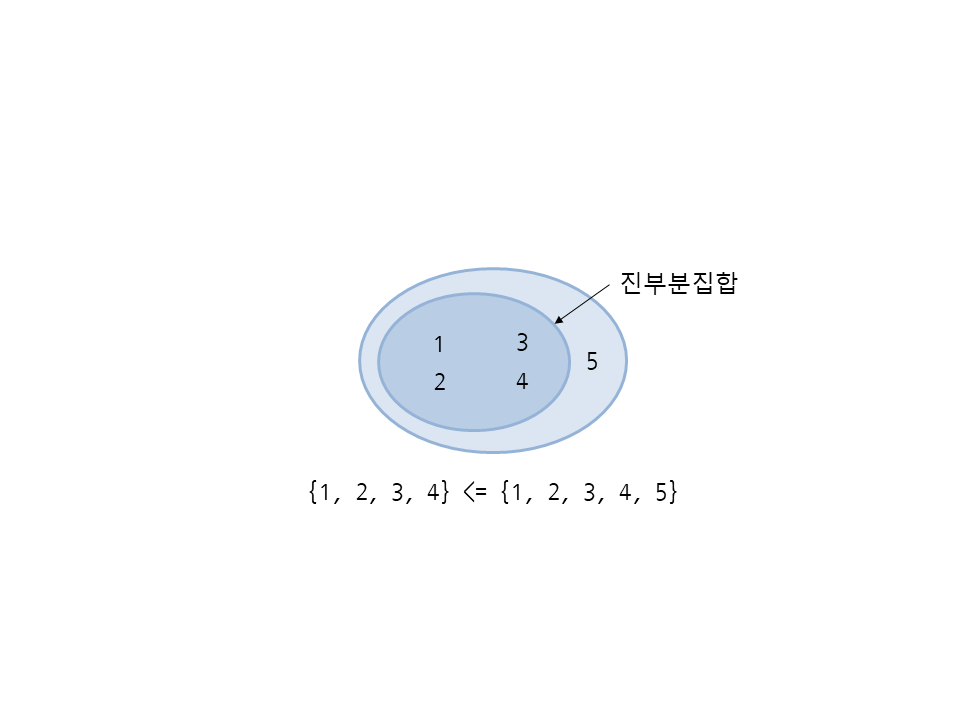
<은 현재 세트가 다른 세트의 진부분집합(proper subset)인지 확인하며 메서드는 없습니다. 다음은 세트 {1, 2, 3, 4}가 {1, 2, 3, 4, 5}의 진부분집합이므로 참입니다. 즉, 부분집합이지만 같지는 않을 때 참입니다.

현재세트 < 다른세트

>>> a = {1, 2, 3, 4}
>>> a < {1, 2, 3, 4, 5}
True

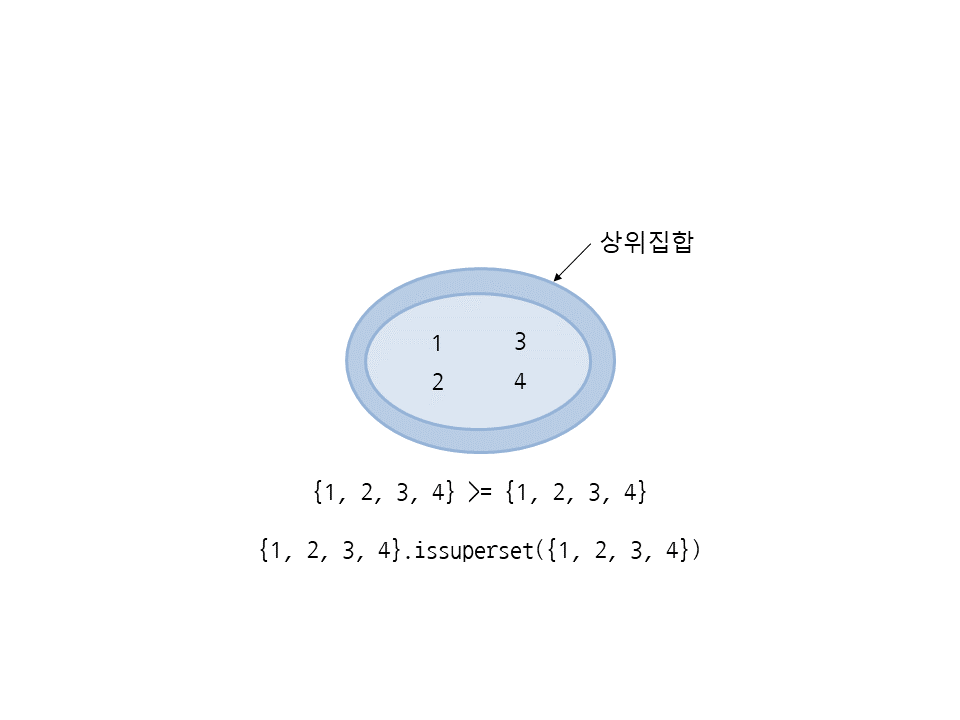
>=은 현재 세트가 다른 세트의 상위집합(superset)인지 확인하며 issuperset 메서드와 같습니다. 다음은 세트 {1, 2, 3, 4}가 {1, 2, 3, 4}의 상위집합이므로 참입니다(등호가 있으므로 두 세트가 같을 때도 참입니다).

현재세트 >= 다른세트
현재세트.issuperset(다른세트)

>>> a = {1, 2, 3, 4}
>>> a >= {1, 2, 3, 4}
True
>>> a.issuperset({1, 2, 3, 4})
True

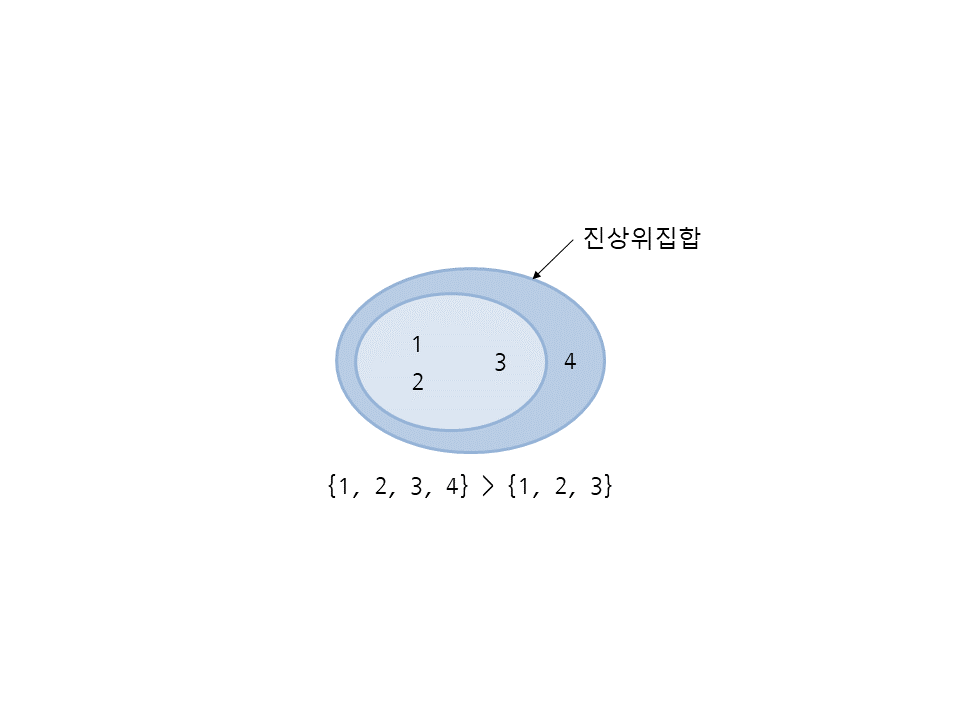
>은 현재 세트가 다른 세트의 진상위집합(proper superset)인지 확인하며 메서드는 없습니다. 다음은 세트 {1, 2, 3, 4}가 {1, 2, 3}의 진상위집합이므로 참입니다. 즉, 상위집합이지만 같지는 않을 때 참입니다.

현재세트 > 다른세트

>>> a = {1, 2, 3, 4}
>>> a > {1, 2, 3}
True

26.2.3 세트가 같은지 다른지 확인하기

세트는 == 연산자를 사용하여 서로 같은지 확인할 수 있습니다.

>>> a = {1, 2, 3, 4}
>>> a == {1, 2, 3, 4}
True
>>> a == {4, 2, 1, 3}
True

세트는 요소의 순서가 정해져 있지 않으므로 ==로 비교했을 때 각 요소만 같으면 참입니다.

!= 연산자는 세트가 다른지 확인합니다.

>>> a = {1, 2, 3, 4}
>>> a != {1, 2, 3}
True

26.2.4 세트가 겹치지 않는지 확인하기

disjoint는 현재 세트가 다른 세트와 겹치지 않는지 확인합니다. 겹치는 요소가 없으면 True, 있으면 False입니다.

현재세트.isdisjoint(다른세트)

>>> a = {1, 2, 3, 4}
>>> a.isdisjoint({5, 6, 7, 8})       # 겹치는 요소가 없음
True
>>> a.isdisjoint({3, 4, 5, 6})    # a와 3, 4가 겹침
False

내비게이션 생략